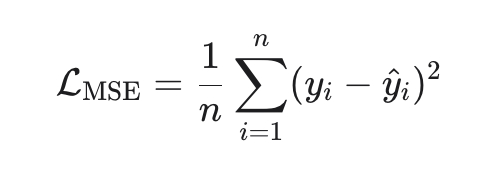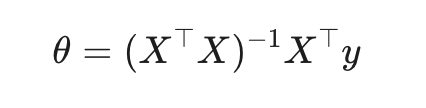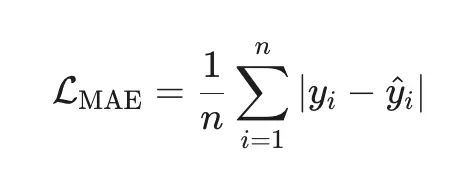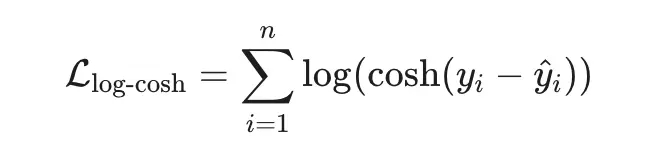Что такое оптимизатор Adam?

Делаю такой клиповый курс «Что такое», где за 20 секунд объясняю термины по разработке нейросетей и искусственному интеллекту.

Если пост наберёт 30 плюсов, продолжу выкладывать другие клипы в сообществе «Наука | Научпоп».

Линейная регрессия — один из самых фундаментальных и широко применяемых методов в машинном обучении. Несмотря на простоту, её эффективность сильно зависит от двух ключевых компонентов:

1. Функции потерь (loss function) — что именно мы минимизируем?

2. Метода оптимизации (solver) — как мы ищем решение?

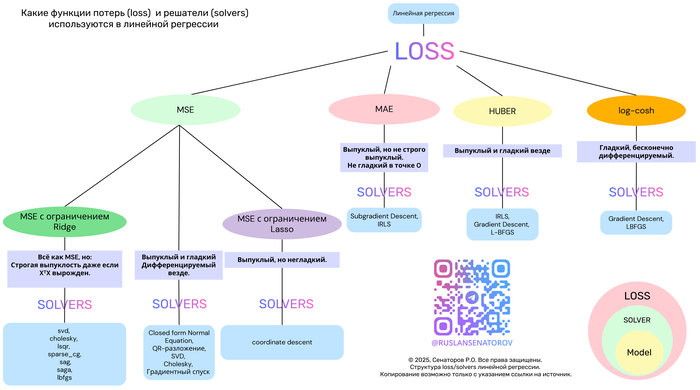
В этой статье мы разберём популярные функции потерь — MSE, MAE, Huber и Log-Cosh — их свойства, плюсы и минусы. А также покажем, как выбор функции потерь определяет выбор алгоритма оптимизации.

Почему функция потерь так важна?

Функция потерь измеряет, насколько предсказания модели отличаются от реальных значений. От её формы зависят:

• Чувствительность к выбросам

• Наличие замкнутого решения

• Выпуклость задачи

• Скорость и стабильность обучения

Давайте сравним четыре ключевые функции потерь в контексте линейной регрессии.

1. MSE (Mean Squared Error) — стандарт по умолчанию

• Эквивалентна максимуму правдоподобия при нормальном шуме.

Замкнутое решение (метод наименьших квадратов):

Плюсы:

Выпуклая, гладкая, дифференцируемая → легко оптимизировать

Минусы:

• Чувствительна к выбросам (ошибки возводятся в квадрат).

Solver:

• Normal Equation (аналитическое решение)

• SGD, SAG, LBFGS (в scikit-learn: solver='auto', 'svd', 'cholesky' и др.)

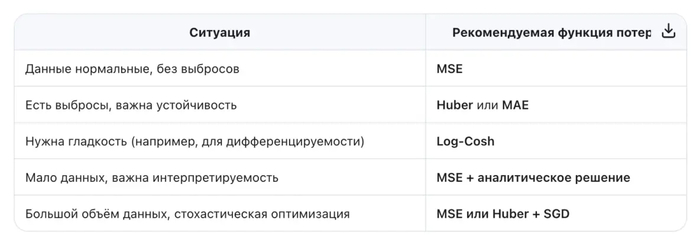
Когда использовать: когда данные «чистые», ошибки гауссовские, и важна интерпретируемость.

2. MAE (Mean Absolute Error) — робастная альтернатива

Плюсы:

• Робастна к выбросам (ошибки в первой степени).

• Минимизирует медиану ошибок (а не среднее).

Минусы:

• Недифференцируема в нуле → нет аналитического решения.

• Требует итеративных методов.

Solver:

• Linear Programming (например, через симплекс-метод)

• Subgradient Descent (в scikit-learn: QuantileRegressor с quantile=0.5)

Когда использовать: когда в данных есть аномалии или тяжёлые хвосты (например, цены, доходы).

3. Huber Loss — лучшее из двух миров

Плюсы:

• Гладкая и дифференцируемая.

• Робастна к выбросам (линейная штраф за большие ошибки).

• Гибкость через параметр δδ.

Минусы:

• Нужно настраивать δδ (часто выбирают как процентиль ошибок).

• Нет замкнутого решения.

Solver:

• Gradient Descent, LBFGS, Newton-CG(в scikit-learn: HuberRegressor с fit_intercept=True)

Когда использовать: когда вы подозреваете наличие выбросов, но хотите сохранить гладкость оптимизации.

4. Log-Cosh Loss — гладкая робастность

Плюсы:

• Гладкая везде (бесконечно дифференцируема).

• Ведёт себя как MSE при малых ошибках и как MAE при больших.

• Устойчива к выбросам, но без «изломов».

Минусы:

• Вычислительно дороже (логарифм и гиперболический косинус).

• Не так распространена в классических библиотеках.

Solver:

• Gradient-based методы: SGD, Adam, LBFGS(в TensorFlow/PyTorch легко реализуется; в scikit-learn — через кастомный регрессор)

Когда использовать:

• когда вы ищете баланс между робастностью MSE и гладкостью MAE.

• Вы хотите избежать чувствительности MSE к выбросам, но сохранить дифференцируемость.

• Вы строите гибридную модель, где loss должен быть всюду гладким (например, для вторых производных).

Правило:

• Если loss квадратичен → можно решить напрямую.

• Если loss неквадратичен → нужен итеративный численный метод.

И помните: нет универсально «лучшей» функции потерь — только та, что лучше всего подходит вашим данным и задаче.